『子供の科学』2022年12月号の「はじめよう ジブン専用パソコン」では、Scratchらしくペンを使って円周率を求める方法を紹介しました。そして、最後にラマヌジャンの円周率公式もプログラムで計算できることを示しましたね。ここでは、具体的に数式をどのようにプログラムすればよいのかを説明します。
1 ラマヌジャンの円周率公式
下が、ラマヌジャンの円周率公式です。小中学生だと見慣れない記号がいくつかありますね。
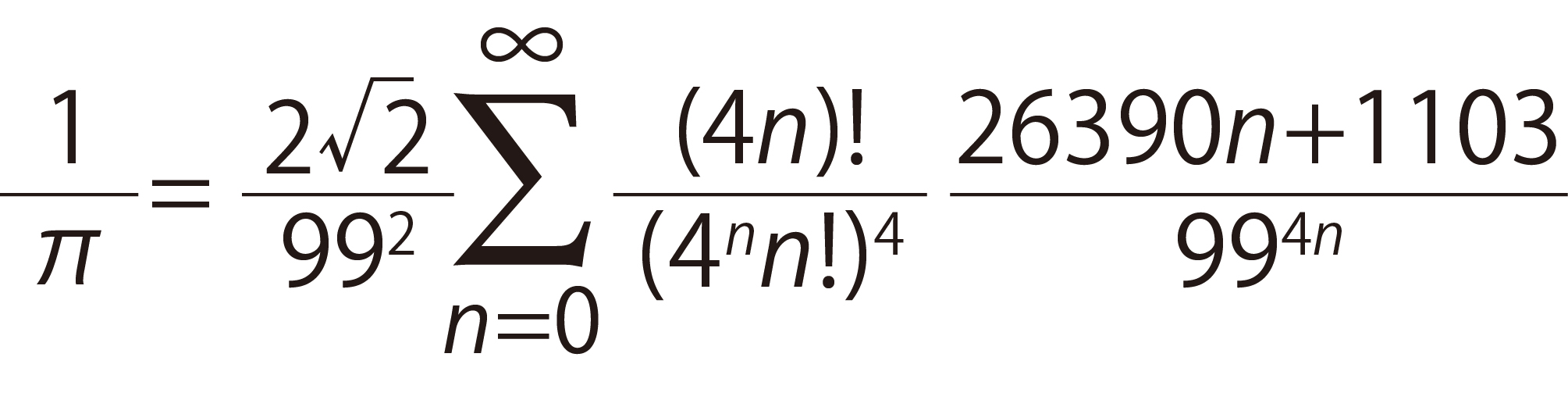
「π 」は円周率、「
」は平方根ですね。「
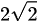」は「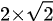
」と同じで「×」が省略されています。「 
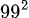」は、べき乗の意味で、99を2回掛けたもの、つまり「99×99」のことです。「
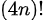」の「!」は階乗といって、たとえば、「5!」は「5×4×3×2×1」になります。
分かりにくいのは、Σ（シグマ）記号を使った「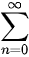 
」ですね。これは、nが0から∞まで、右の式（項）を足し合わせるということです。たとえば、「 
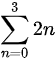」は「2×0+2×1+2×2+2×3」です。このような数を級数と言い、特に無限（∞）の項があるものは無限級数と呼ばれます。
この式をScratchのプログラムで表すことを考えてみましょう。「演算」カテゴリーに平方根はありますが、べき乗、階乗、Σはありません。逆にいうと、これらをつくればよいことになります。
2 べき乗をつくる
べき乗を実装するアルゴリズムはいくつかありますが、ここでは一番シンプルな反復（繰り返し）を使ってみます。その際、非負整数（0と自然数）のみを扱うことにします。
では、「べき乗」を「ブロック定義」でつくりましょう。ブロック名は「(a)の(b)乗」としました。その際、Scratchのブロック定義は返り値を持てないので、あらかじめ「このスプライトのみ」の変数として「べき乗の答え」をつくっておきます。変数は「変数」カテゴリーの「変数を作る」でつくることができます。
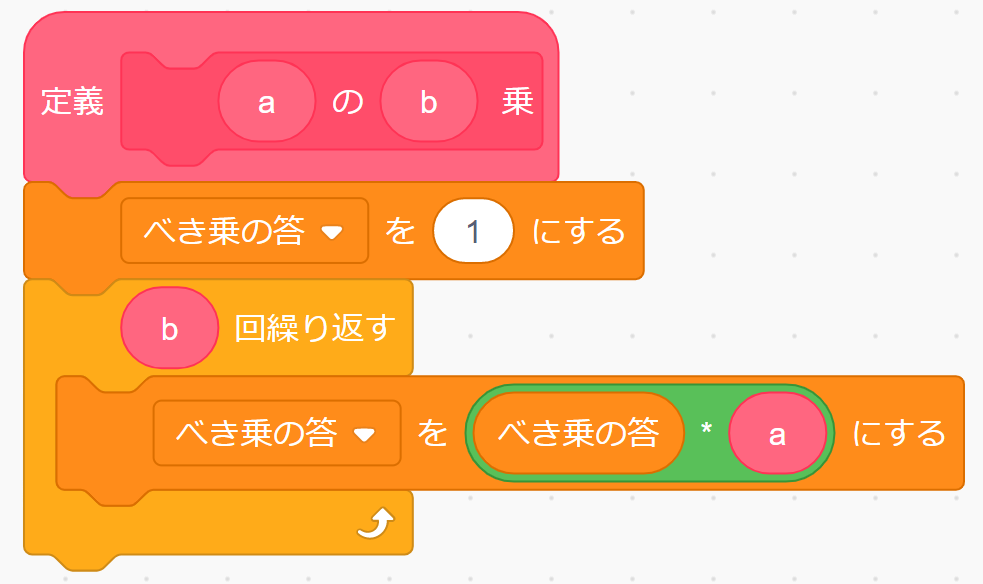
上のプログラムを見てみましょう。「べき乗の答え」を「1」で初期化してから、「べき乗の答え」に「a」をかけたものを「べき乗の答え」に代入することを「b」回繰り返していることがわかりますね。
たとえば、「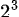
」は次のように表され、実行すると「べき乗の答え」は「8」になります。
3 階乗をつくる
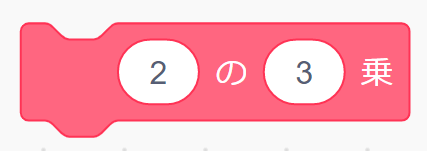
階乗は再帰（ある関数の中で、その関数自体を呼び出すこと）でつくる方法もありますが、これも反復でつくってみます。定義するブロックの名前は「(n)の階乗」としました。ここでも、非負整数のみを対象にします。使っている変数の「階乗の答」と「カウンター」は「このスプライトのみ」で用意しておきます。
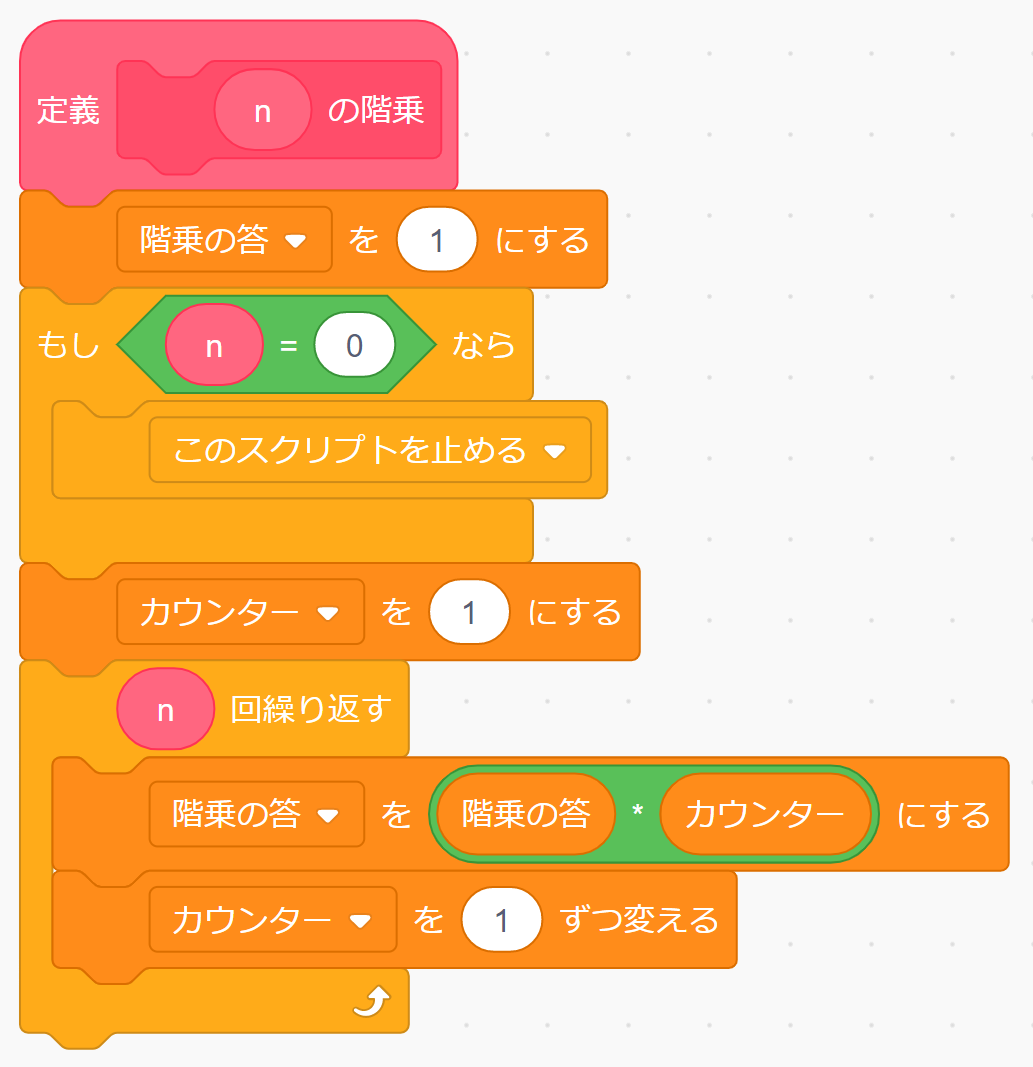
「n」が「0」の時に答えを「1」にしているのは、階乗の定義（空積の規約）によるものです。あとは、回数を数える「カウンター」を1からはじめて、「階乗の答」と「カウンター」をかけたものを「階乗の答」に代入することを「n」回繰り返していますね。
たとえば、「5!」は「(5)の階乗」なので、次のブロックを実行すると、「階乗の答」は「120」になります。
4 全体を組み立てる
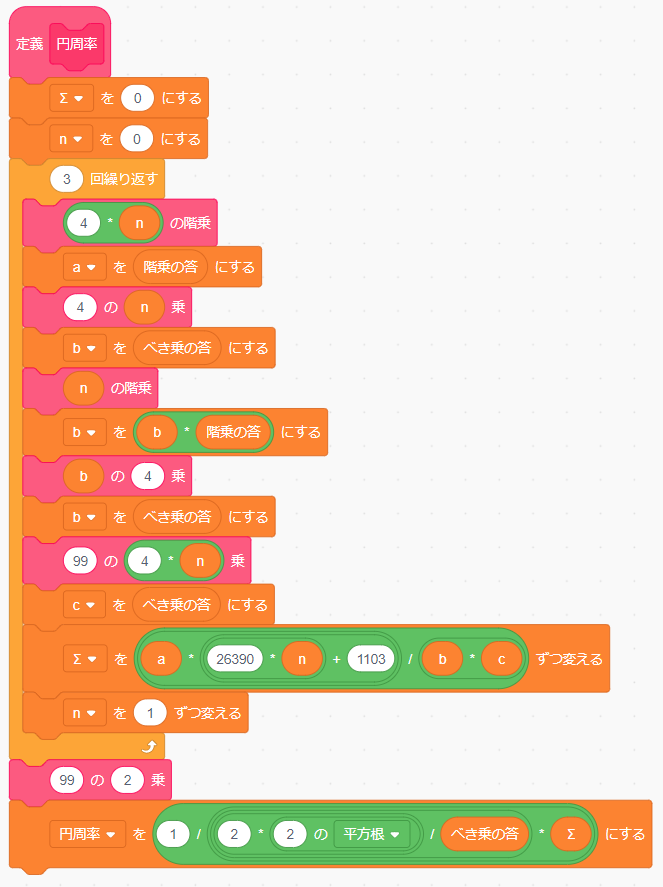
あとは式の通りに全体を組み合わせれば完成です。そのために「円周率」というブロックを定義します。
ここでは、
変数「a」を「 」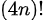
変数「b」を「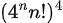
」
変数「c」を「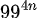
」
として、それぞれ「このスプライトのみ」の変数で用意しています。「Σ」、「n」、「円周率」も同じように変数をつくります。
一見すると複雑に見えると思いますが、ひとつひとつ見ていくと数式と対応していることがわかると思います。
ただし、本来は無限級数なので繰り返し回数は無限大、つまり「ずっと」のはずですが、ここでは3回としています。
5 円周率を求める
円周率を求めるには次のプログラムを緑の旗をクリックして実行します。「言う」内容を「( )と(円周率)」にしているのは、変数を数値として表示すると小数点以下2桁で丸められるので、文字列にして回避するためです。
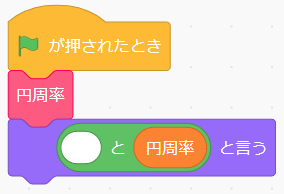
この結果を2022年11月号の付録「円周率10000桁ポスター」で確認すると、小数点以下15桁まで合っていることがわかります。わずか3回の繰り返しでこのように精度が高い（収束が早い）のが、ラマヌジャンの円周率公式の特徴です。
残念ながら、Scratchの変数の精度ではこれ以上繰り返しても桁数を増やすことができません。多倍長計算という手法を使うと桁数を増やせるので、興味がある人は調べてみましょう。
文
コカネットプレミアム（DX）会員は、雑誌『子供の科学』バックナンバー電子版が読み放題！ 以下をクリック☆
